Função Afim e a composição da conta de água

ÁGUA: CONDIÇÃO DE EXISTÊNCIA À VIDA

1.      Situação-problema:

A composição da conta de água pela CORSAN (Companhia Riograndense de Saneamento) de uma residência cuja área construída é maior que 60 m² e o consumo mensal menor que 20 m³, conforme dados da CORSAN  no ano de 2015, é da seguinte maneira:  

R$ 19,35 fixos,       acrescido de  R$ 4,09 por m³ consumido no respectivo mês Cfe tabela tarifária Corsan / 2015

www.corsan.com.br/

2. Considerando as contas de água,    Tabela da CORSAN e os  Dados da Conta de água  ( Fatura ):  

·         Categoria:  RB  ( Residencial Básica )

·         Mês / Ano :

·         Consumo em metros cúbicos:

·         Consumo em litros:

3.  Elabore uma expressão, que relacione o Preço a pagar ( em reais ) e quantidade de água consumida ( em metros cúbicos ) no respectivo mês .

4.  Cálculos utilizando a Lei da Função e a fatura:

          

               4.1.      Exemplo de cálculo cujo consumo mensal é menor ou igual a 20 m³ :

                                               Fatura de MARÇO / 2015: 

                                                Consumo:  13 m³

                                                Serviço Básico ( SB ) = R$ 19,35

                                                Preço Base ( PB ) =      R$   4,09

Total a pagar = 19,35 + 4,09 . ( consumo )

y = 19,35 + 4,09 . x

                                                                                         

                                                                  y = 19,35 + 4,09 . ( 13 )

                                                                   y = 19,35 + 53,77

                                                                   y = R$ 72,52

                     4.2.  Gráfico no GeoGebra:

  

          4.3. Fatura com excesso de consumo   ( consumo ≥ 21 m³ ) conforme Tabela de Exponenciais: 

http://www3.corsan.com.br/informacoes/tab_exponencial.htm

   Exemplo de cálculo cujo consumo mensal é maior que  20 m³ :

                                       Novembro / 2014

                                                                Consumo: 34 m³

                    Lei da Função cfe tabela de tarifas da Corsan:    http://www.corsan.com.br/node/18

                   Total a pagar = PB x C ⁿ + SB, sendo          PB = Preço Base ( R$ 4,09 )

                                                                      

                                                                     C = Consumo em m³

                                                                      n = valor cfe “tabela de exponenciais”

                                                                      SB = Serviço Básico ( R$ 19,35 )

                  calculando:

                  Total = PB x C ⁿ + SB

                  Total = 4,09 . ( 34 ^1,09  )  +  19,35

                  Total = 4,09 . ( 46,69 ) +  19,35

                  Total = 191,00  + 19,35

                  Total = R$  210,35

          5.   Qual situação é mais vantajosa?

Dividir a conta de água de duas famílias que moram no mesmo terreno:

a)      Com apenas um registro de água?

b)      Contendo dois registros, um para cada casa?

Exemplo do valor da conta    ( x = 30 m³ )   dividida entre  duas famílias.

Situação 1: ·          Consumo = 30 m3 ·         Conta dividida entre DUAS FAMÍLIAS ·         Apenas UM REGISTRO DE ÁGUA Total = PB x C n + SB Total = 4,09 . ( 30 1,09 )  +  19,35 Total = 4,09 . ( 40,74 ) +  19,35 Total = 166,64  + 19,35 Total = R$ 185,99 Total = 185,99 : 2 Total = R$ 92,99 por família	Situação 2: ·          Consumo = 30 m3 ·         Conta dividida entre DUAS FAMÍLIAS  ·         DOIS REGISTROS DE ÁGUA                   y = 19,35 + 4,09 . x                                                                                                              y = 19,35 + 4,09 . ( 15 )                    y = 19,35 + 61,35        y = R$  80,70 por família
A diferença paga é de R$ 12,29 por mês. Em um ano a diferença é de R$ 147,12.

6. Mais alguns cálculos que foram desenvolvidos  utilizando a conta de água:

·         Histórico de consumo em m³ e em litros  dos últimos 6 meses

·         Número de moradores da casa

·         Dias de consumo no  mês

·         Média Diária por morador em m³  e em litros

  7. Algumas fotos:

Essas atividades foram desenvolvidas em parceria com os bolsistas do PIBID ( Programa Institucional de Iniciação à Docência - “Subprojeto de Matemática Recursos e práticas motivadoras e suas diferentes formas de comunicação no ensino da Matemática” – IFRS,  Câmpus Ibirubá- RS.

Atividades Computacionais no estudo de Funções

Descrevo aqui situação-problema desenvolvida em de sala de aula de 1ª série do Ensino Médio, ao desencadear o conceito de Funções, utilizando os aplicativo Excel e Graphmatic para construção de gráficos.

Os alunos das terceiras séries do Ensino Médio da nossa Escola são responsáveis pelo bar da Escola, que funciona no recreio dos três turnos. O lucro arrecadado será destinado ao pagamento das despesas com a viagem de estudos que está programada para o final do ano letivo. Um dos produtos vendidos na cantina é o pastel, ao preço de R$ 1,50 a unidade. Considerando a situação acima, responda:
1) Qual o valor arrecadado, em reais, se vender:
a) 10 pastéis? b) 20 pastéis? c) 30 pastéis? d) 40 pastéis?
2) Elabore uma tabela relacionando os valores trabalhados acima: quantidade de pastéis vendidos e valor arrecadado ( em reais ).



3) A partir desses cálculos, obter a expressão que relacione o valor recebido em função do número de pastéis vendidos.
V = 1,50 p
O valor arrecadado depende da quantidade de pastéis vendidos.
O valor arrecadado é função da quantidade de pastéis vendidos.

4) Representar graficamente a tabela elaborada:



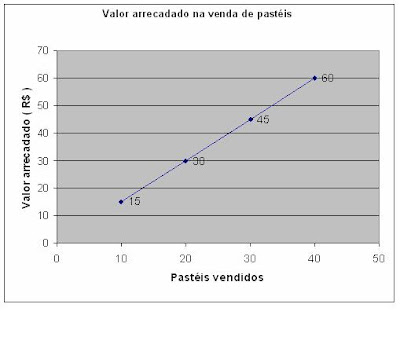
5) Considerando que o pastel é comprado pela 3ª série ao preço de R$ 0,75 e revendido a R$ 1,50 a unidade e, em média são colocados à venda 100 pastéis por dia, eterminar:

6) Qual é a despesa diária da 3ª série com a aquisição dos 100 pastéis para a venda na cantina?
D = 0,75 . 100
D = 75,00

7) Qual o valor arrecadado na venda de:
7.1) 30 pastéis? R$ 45,00
7.2) 40 pastéis? R$ 60,00
7.3) 50 pastéis? R$ 75,00
7.4) 60 pastéis? R$ 90,00
7.5) 70 pastéis? R$ 105,00
7.6) 80 pastéis? R$ 120,00
7.7) 90 pastéis? R$ 135,00

7.8) Se forem vendidos 30 ou 40 pastéis a cantina terá lucro ou prejuízo?
De quanto?
7.9) E se forem vendidos 50 pastéis? Qual é o valor do lucro ou prejuízo?
7.10) Vendendo 60, 70, 80 ou 90 pastéis, o que acontece: lucro ou prejuízo? De que valor?
Sabemos que:
LUCRO = VALOR ARRECADADO - DESPESA

Através destes dados como podemos elaborar uma expressão para o cálculo do lucro obtido pela 3ª série na venda dos pastéis?
L ( p ) = 1,50 p – 75,
onde p = número de pastéis vendidos e
L(p) = lucro obtido.
Uma função dada por f ( x ) = ax + b chama-se função afim, onde a, b R e a 0.

8) Represente graficamente o lucro obtido através da expressão
L ( x ) = 1,50 x - 75, atribuindo a x ( número de pastéis vendidos ), os valores 30, 40, 50, 60, 70, 80 e 90, já calculados anteriormente.
Observando as respostas da questão nº 8, quantos pastéis devem ser vendidos para pagar a despesa de R$ 75,00 por dia, realizada pela 3ª série?

Despesa/dia = R$ 75,00
Preço do pastel = R$ 0,75
Nº de pastéis que devem ser vendidos = 50
Ou seja, vendendo 50 pastéis por dia não se tem nem lucro nem prejuízo.



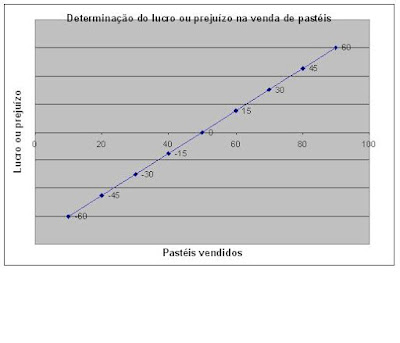
9) Localize, no gráfico, o ponto que determina a resposta da questão anterior.
P ( 50, 0 )
Então:
x = 50
y = 0

10) Chama – se zero ou raiz da função f(x) = ax + b o valor de x que anula o função, isto é, torna f(x) = 0. Na função L ( p ) = 0,75p - 75 , o zero ou raiz da função é x = 50, pois f(x) = 0. O zero da função, no gráfico, fica no eixo das abscissas.

Graficamente significa que o zero da função L ( p ) = 0,75p - 75 é a abscissa do ponto em que a reta corta o eixo x.


ATIVIDADES COMPUTACIONAIS
1) Representar graficamente, no aplicativo Excel, as funções definidas por:
1.1) y = 0,60x, relacionando a quantidade de pastéis vendidos (10,20,30,40) e o valor arrecadado, em reais, referente ao problema da venda de pastéis.
1.2) y = 0,75x – 75, relacionando a quantidade de pastéis vendidos (30, 40, 50, 60, 70, 80, 90) e o lucro obtido, em reais, referente ao problema da venda de pastéis.
2) Através do aplicativo Graphmatic, trace o gráfico da função y = x ( função mãe). Trace os gráficos das funções y = ax atribuindo ao parâmetro “a” diferentes valores. Compare estes gráficos com o gráfico da função mãe e formule uma conclusão a respeito das alterações ocorridas com a variação deste parâmetro.
3) Obtenha o gráfico da função y = ax + b mantendo o parâmetro a constante e variando “b”. Comparando com o gráfico da função mãe, qual o significado deste parâmetro nos gráficos obtidos? Determine o ponto ( x, y ) onde cada gráfico corta o eixo x e também o eixo y.
4) Obtenha o gráfico de funções Afim e Lineares.
Classifique-as como crescente ou decrescente.
Localize, em cada gráfico, o zero da função e o coeficiente linear.
( Fazer o registro das conclusões relativas aos exercícios 2, 3 e 4 no caderno ).

Regras de Etiqueta na Internet

Netiqueta é um conjunto de regras a serem observadas nas diversas ferramentas de comunicação que a Internet oferece. Não são oficiais, isto é, não estão documentadas em algum lugar. É uma compilação de normas escritas e expandidas pelos próprios usuários da Internet afim de evitar mal-entendidos em comunicações via internet.
Deste conjunto de normas de conduta online, podemos destacar algumas:
• Combine letras maiúsculas e minúsculas, da mesma forma que na escrita comum. Cartas em papel não são escritas somente com letras maiúsculas; na Internet, escrever em maiúsculas é o mesmo que gritar!
• Para enfatizar frases e palavras, use os recursos de_sublinhar_ (colocando palavras ou frases entre sublinhados) e *grifar* (palavras ou frases entre asteriscos). Frases em maiúsculas são aceitáveis em títulos e ênfases ou avisos urgentes.
• Evite ao máximo usar emoticons de letras, palavras e coisas do gênero;, isso torna a leitura das mensagens muito difícil e confusa, devido ao tempo que precisamos esperar pra que esses emoticons sejam carregados e à irregularidade nos tamanhos e cores. Emoticons expressam emoções, e não palavras, procure usá-los fora das mensagens escritas.
• Ao encaminhar um e-mail que recebeu, por exemplo, remova os e-mails presentes, das outras pessoas. Procure escrever os seus destinatários no campo "CCO” em vez do campo "Para". Este campo esconde os endereços dos destinatários. Todos irão receber, mas ninguém além de você saberá quem mais recebeu a sua mensagem. Ao não fazer o recomendado acima, você está contribuindo para o spam com e-mails dos seus próprios conhecidos. Os endereços de e-mail acumulados serão "pescados" quer por parte dos destinatários quer por empresas especificas existentes na Net cuja função é acumular contatos de e-mail para envio de propaganda não solicitada.
• A linha Assunto ou Subject deve estar sempre preenchida com o assunto tratado em sua mensagem de e-mail.
• Envie arquivos anexados apenas quando solicitado, e jamais para listas.
• É boa prática deixar linhas em branco entre blocos de texto. Dessa forma, o texto fica organizado e mais fácil de ler, mesmo que a mensagem seja longa.
• Procure responder a todas as mensagens pessoais. Lembre-se de agradecer às pessoas que o ajudarem. Mas não inclua todo o conteúdo da mensagem respondida; deixe o suficiente apenas para indicar os pontos que você está comentando.
• É possível criar o que se chama "assinatura" para suas mensagens de correio eletrônico. As assinaturas são arquivos pequenos, contendo alguma informação sobre você: nome completo, empresa, cargo, referências de trabalhos on-line, frases. Não exagere! Essa assinatura deve se restringir a no máximo 4 (quatro) linhas.
• Divulgar produtos ou serviços é arriscar-se a receber flames. Introduza divulgações no contexto das conversas.
Enviar divulgação não desejada é uma das formas de spam.Em vez de enviar propagandas, use alternativas: endereços de sites nas assinaturas de e-mail, ou participação em listas e endereços na Internet dedicados à divulgação de propagandas.
• Fazer spam é enviar mensagens por e-mail para dezenas de pessoas, listas ou newsgroups, não importando o assunto da lista, ou o interesse das pessoas destinatárias das mensagens.
A prática de "spamming" não é um mero fator de aborrecimento para os internautas, pois chega a ser prejudicial: ao espalhar mensagens em diversos pontos de distribuição, muitas pessoas de uma mesma rede podem receber várias cópias, causando a sobrecarga das caixas de e-mail, entre outros transtornos.
Ao receber mensagens com alertas sobre vírus, correntes de qualquer tipo,histórias estranhas, não passe adiante. Comente com amigos que já tenham mais experiência, com o suporte de seu provedor, ou responsáveis pelo equipamento utilizado.

Fonte: http://www.icmc.usp.br
http://pt.wikipedia.org

Fractais

Homem Vitruviano

O belo e as formas perfeitas é algo que o Homem valoriza desde a Antiguidade  e a Matemática é um saber que vem sendo construído acompanhando a evolução da humanidade. É uma ciência presente, de alguma forma, em todas as outras, contribuindo de maneira relevante no processo de desenvolvimento da sociedade. 

Nesse contexto, a busca pelo belo e pela perfeição, os estudiosos deparam-se com o número Phi,  também denominado Número de Ouro ou Número Áureo, representado pela letra grega  Φ  ( phi )  (lê-se fi), em homenagem a Phideas (séc.V a.C.), cujo valor é 1,618033988749 .  . , o qual arredondamos para 1,618.  Phi é a raiz positiva  da equação  x² – x – 1 = 0 .

Encontramos  várias ocorrências do número Phi na natureza.

No corpo humano, ao determinarmos o quociente entre as dimensões abaixo, obteremos um valor aproximado ao número Phi.

§                     A altura do corpo humano e a medida do umbigo até o chão.

§                     A altura do crânio e a medida da mandíbula até o alto da cabeça.

§                     A medida da cintura até a cabeça e o tamanho do tórax.

§                     A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.

§                     O tamanho dos dedos e a medida da dobra central até a ponta.

§                     A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.

§                     A medida do seu quadril ao chão e a medida do seu joelho até ao chão.

§                     A medida do cotovelo até o pulso e a medida do seu pé

Na população de abelhas:  a população entre abelhas fêmeas e machos em qualquer colméia.

Na Arte,  a proporção áurea foi muito usada, em obras como O Nascimento de Vênus,  quadro de Botticelli, em que Afrodite está na proporção áurea. Esta proporção estaria ali aplicada pelo motivo do autor representar a perfeição da beleza.

Em O Sacramento da Última Ceia de Salvador Dalí, as dimensões do quadro (aproximadamente 270 cm × 167 cm) estão numa Razão Áurea entre si. Na história da arte renascentista a perfeição da beleza em quadros foi bastante explorada com base nesta constante. Vários pintores e escultores lançaram mão das possibilidades que a proporção os dava de retratar a realidade com mais perfeição.

Em “A criação do Homem”,  de Michelangelo que ilustra o teto da Capela Cistina, em Roma,  falange, a falanginha e a falangeta do dedo indicador têm comprimentos que estão na proporção áurea.
       A Mona Lisa de Leonardo da Vinci utiliza o número áureo nas relações entre seu tronco e cabeça, e também entre os elementos do rosto.

Na  Literatura, o número de ouro  está presente de forma mais notável  no poema épico grego Ilíada , de Homero , que narra os acontecimentos dos últimos dias da Guerra de Tróia. pois existe a proporção entre as estrofes maiores e as menores, resultando num valor aproximado a 1,618, o número de ouro.

Em Os Lusíadas, Camões divide a obra na razão de ouro no ponto em que anuncia a chegada à Índia.

Através do conhecimento da relações que regem o corpo humano, Da Vinci criou o Homem Vitruviano, que representa a maior parte das ocorrências do número Phi no em nosso corpo. É usado como referência de estética, de simetria e proporção. Nessa ilustração (figura acima),  a área total do círculo é idêntica à área total do quadrado.

O Homem Vitruviano transformou-se em um ícone de beleza e estética até os nossos dias. Esse conceito de proporção humana influenciou a estética de muitos pintores, arquitetos e engenheiros. Muitos dos prédios “clássicos” que viriam a definir o estilo europeu ocidental foram construídos influenciados por essas idéias de proporção.

Fonte: http://pt.wikipedia.org/

A educação matemática e o uso do computador

Novas exigências são colocadas para a formação do cidadão em função do progresso científico e tecnológico. É exigida maior precisão produtiva e padrões de qualidade de produção mais desenvolvidos, no mercado de trabalho. Iniciativa e autonomia para resolver problemas que se colocam face aos novos desafios da sociedade, entendimento do trabalho como um todo, utilização as diferentes tecnologias e linguagens são condições essenciais para o sujeito que quer ingressar no trabalho. Entendemos assim, que cada vez mais a sociedade depende do conhecimento.

           Em vista disso, a escola tem o compromisso de dar sua contribuição à sociedade, e a Matemática integra-se a este novo desafio, desenvolvendo metodologias que enfatizem competências necessárias à formação do cidadão, por meio de signos e regras que são transformados em linguagem de comunicação de idéias, permitindo modelar a realidade e interpretá-la. Cabe ao professor transformar a realidade que o aluno traz para a sala de aula, mediando os conhecimentos para que o aluno entenda o mundo e busque formas de transformá-lo. E, na medida que as atividades escolares são aplicadas na intenção de que o educando desenvolva as capacidades de refletir, produzir e criar, entendendo que há o desenvolvimento de novas formas de operações mentais, modifica sua relação cognitiva com o mundo.

As tecnologias, em suas diferentes formas e usos, constituem um dos principais agentes de transformação da sociedade, e a informática é apontada como instrumento que traz um grande leque de possibilidades ao processo de aprendizagem da matemática.

Os aplicativos podem ser usados para fazer a introdução de um determinado conhecimento, desencadeando conceitos,  como também,  para reforçar e comprovar saberes.

Acredito que, ao utilizarmos mais este recurso como ferramenta na construção do conhecimento, diversificamos as possibilidades no fazer pedagógico. Através de atividades computacionais e de diversos aplicativos,  elaboramos  gráficos, desencadeamos conceitos de Geometria,  estudamos Álgebra, enfim, desenvolvemos saberes e justificamos integração da informática ao processo de construção de conhecimento, na perspectiva da compreensão e evolução da humanidade, uma vez que  nosso aluno certamente enfrentará ou já enfrenta um mercado de trabalho que envolva as novas possibilidades em termos de tecnologia que aí surgem.

O desenvolvimento rápido da tecnologia, requer trabalhadores habilitados, dotados de iniciativa, preparados para aprender a aprender e buscar soluções criativas para resolver problemas que surgem, assim como dispostos a enfrentar uma contínua formação, pois o que se exige para a inserção no atual mercado de trabalho é um nível de formação cada vez mais elevado; um sujeito capaz de ler, interpretar, analisar, argumentar, calcular, raciocinar e compreender. A escola precisa desenvolver uma prática pedagógica que contribua para a formação deste cidadão. Da mesma forma, cabe à escola oportunizar situações de convívio social onde se aprenda a ter respeito mútuo, bom senso, responsabilidade, criticidade e solidariedade.

Repensando o Ensino de Matemática na Educação Básica

O ensino de  Matemática, tem merecido especial atenção dos educadores, no sentido de superar alguns pontos críticos como a dificuldade na compreensão dos conceitos, bem como  ser considerada fator de exclusão e retenção na educação básica. Acreditamos que conhecimentos desenvolvidos como processos repetitivos e mecânicos, através de  um conjunto de fórmulas e regras prontas,  sem possibilitar reflexão e nem a compreensão crítica da realidade, tem sido uma das causas das críticas à escola atual, no que   tange à qualidade do ensino. Em vista disto estamos promovendo uma reflexão sobre a construção de conceitos matemáticos de forma significativa, relacionando os conteúdos com atividades do cotidiano,  buscando sentido para o aluno,  problematizando e contextualizando, sem que o educando sofra restrições e limitações no acesso ao conhecimento. Fazer com que os conteúdos tenham significado, requer que se dê um novo enfoque ao ensino de Matemática, diferente do usual, relacionando os conteúdos às aplicações com outras ciências, com o cotidiano e também com a própria Matemática, justificando a emergência  dos conteúdos do ponto de vista de sua história e da história da humanidade. A Matemática ao ser desenvolvida de forma que a dúvida, a experimentação e a pesquisa sejam estimuladas em sala de aula, exercitando a argumentação num debate, o raciocínio ágil e coerente, assim como aqueles que a construíram, desenvolverá também a organização do pensamento e o raciocínio.